​π=4？这也太神奇了吧！

π=4？这也太神奇了吧！

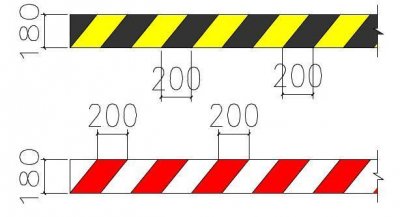
首先，我们画一个直径d=1的圆，再画一个边长1的正方形，如下图所示，这个很容易理解，这个正方形刚好是圆的外切正方形。

如果，我们把正方形的四个角割掉，形成下图所示的图形，显然这个图形的周长依然等于原来的周长。

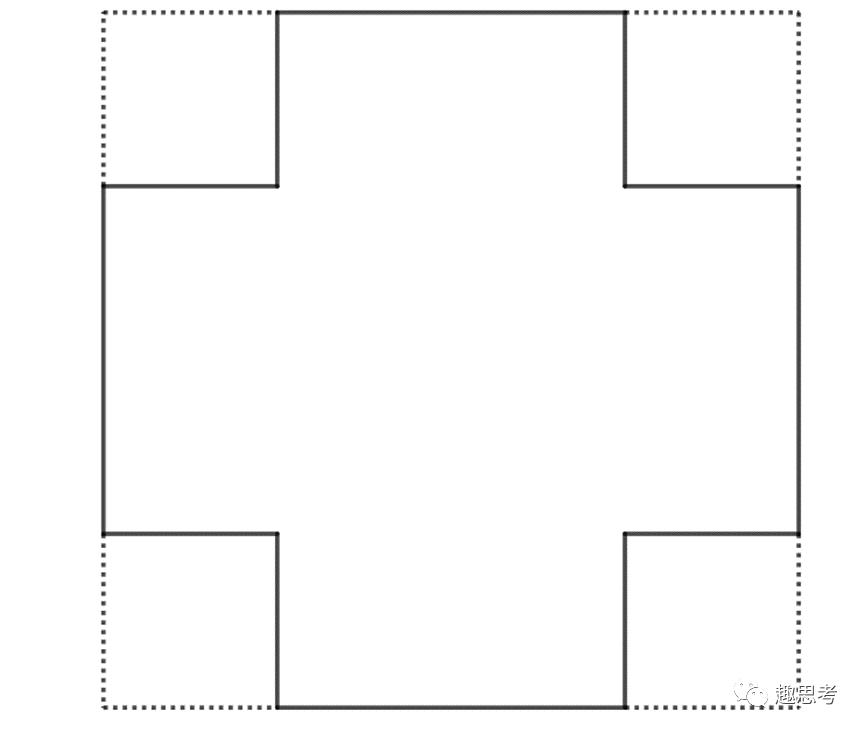
顺着这个思路，我们把圆的外切正方形按照这样的方式割掉四个角，如下图所示，割完之后外围图形的周长依然等于原来正方形的周长。

我们依然顺着这个思路，不断地分割下去，直到分割无穷多次，外围的图形的周长依然等于正方形的周长。从下图观察可知，每一次分割都使得外围图形更接近圆，直到无穷多次分割，外围图形看起来就是个圆。

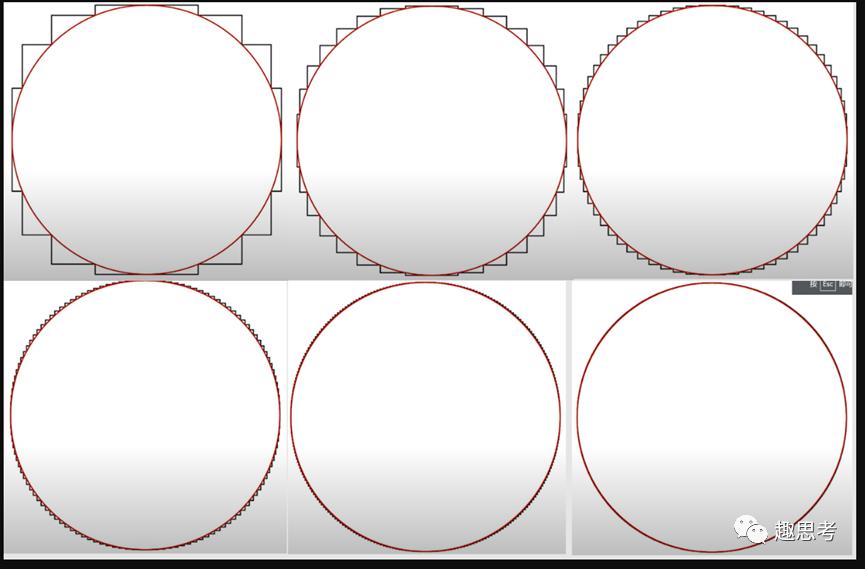
我们知道圆的周长 。外围图形的周长等于正方形的周长=4*边长=4。无数次重复上面的步骤，最终看起来外围图形变成了圆，所以，圆的周长也等于外围图形的周长，所以，最终得出 π=4。

显然，这个和我们一直以来学习的π的值是不一样的，那么，上面的逻辑哪里有问题呢？

问题就出在了进行无数次分割之后，外围图形不是个圆。只是因为，分割的次数多了，视觉上看起来好像是圆。如果，我们有一个无穷大的放大镜，我们用这个无穷放大镜去看一下局部的情况，会是什么样子的呢？就像下面的这个图形。

经过无穷多次分割，分割之后，假设每条小边的长度等于1/n,虽然，n趋近于无穷大，每条边长趋近于0，但是两条小边之和依然大于第三边，第三边的长度 ,虽然，第三边的长度也是趋近0，但是这两个值是不一样大的，所以，经过无穷多次累加之后的结果也不会是一样大。这里不用考虑无穷的概念，通过无穷大镜放大局部就很好理解，这实际上是微分的思想。微分发展过程中的确在遇到无穷大、无穷小这些概念时遇到过麻烦，有一些很有意思的关于无穷概念的思维实验，后面的文章中给大家分享。

（此处已添加书籍卡片，请到今日头条客户端查看）