阿基米德多面体
阿基米德多面体
作者 | 扬帆起航552来源 | 小谜题大世界

阿基米德多面体
阿基米德多面体,简称阿基米德体,是一种高度对称的半正多面体。它是以两种及以上的正多边形为面的凸多面体,并且都是可以从正多面体经过截角、截半、扭棱等操作构造,如下图[1][2]。阿基米德体共有13种,其每条边的长度相同,每个顶点也都全等。阿基米德体因阿基米德的研究而命名(虽然其研究记录已遗失)。

注:
*1-18:1.正四面体 2.正六面体 3.正八面体 4.正十二面体 5.正二十面体 6.截角四面体 7.截角立方体 8.截角八面体 9.截角十二面体 10.截角二十面体 11.截半立方体 12.截半十二(二十)面体 13.小斜方截半立方体 14.大斜方截半立方体 15.小斜方截半十二(二十)面体 16.大斜方截半十二(二十)面体 17.扭棱立方体 18.扭棱十二面体(最后两个有镜像形式,算作一种)。
*对偶:若一种多面体的每个顶点均能对应到另一种多面体上的每个面的中心,二者就互为对偶关系。
*截半:也叫全截角,是指把正多面体的每个角从中点处开刀的去角方式,此时原多面体的每条棱都只剩下一个点。
*截角:也叫均匀截角,是指精心选择下刀处,使得每条棱所剩的长度都和截面边长相等的去角方式。
*扭棱:把正多面体的每个面往外拉出,同方向扭转一定角度,然后用等边三角形填补中间的空隙。
为了方便观察,给出13种阿基米德体的一种展开图:













最后,给出阿基米德体及其对偶多面体——卡塔兰体的对比图[2]。
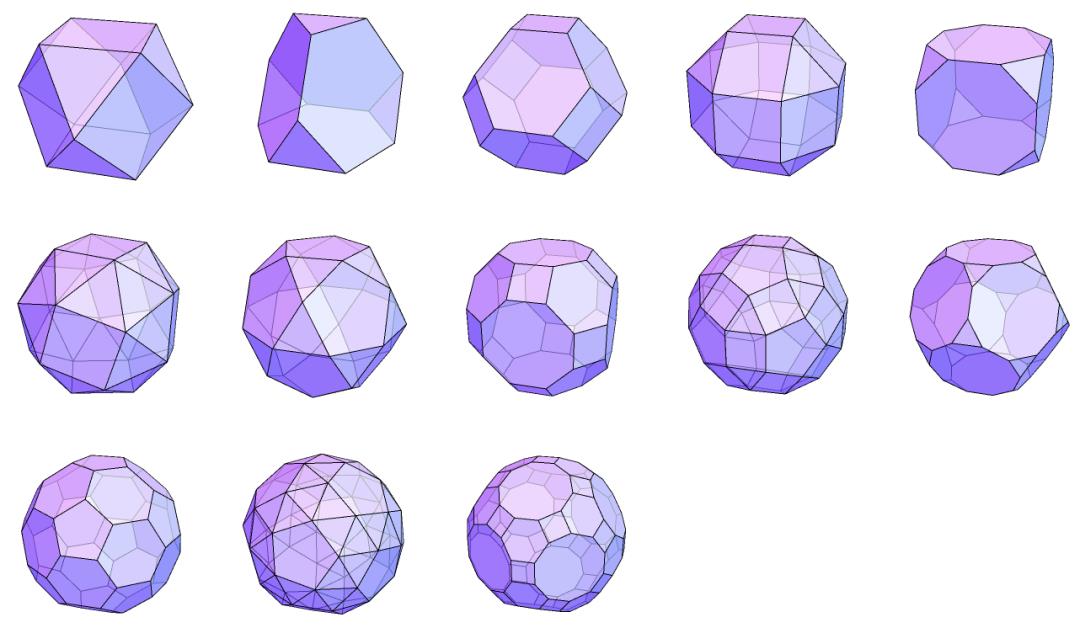
13种阿基米德体(图片来源:参考文献1)
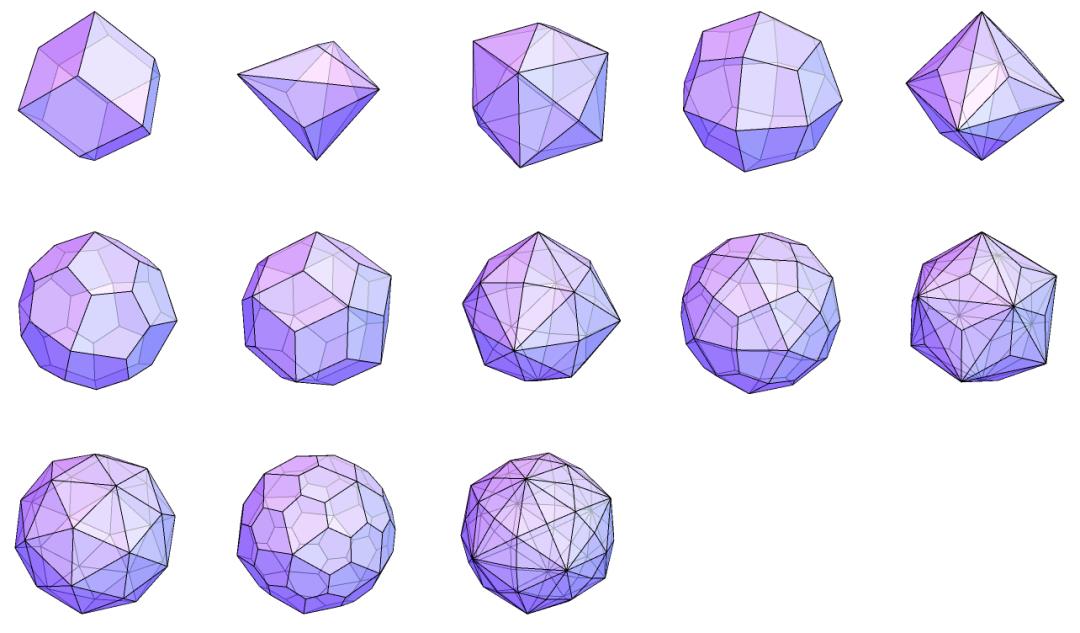
13种卡塔兰体(图片来源:参考文献1)
参考资料:
1.高度对称的多面体和它们的对偶多面体.顾森
http://www.matrix67.com/blog/archives/6161
2.阿基米德多面體.万维百科
https://www.wanweibaike.com/wiki-%E9%98%BF%E5%9F%BA%E7%B1%B3%E5%BE%B7%E5%A4%9A%E9%9D%A2%E9%AB%94